Exponenciální růst a pokles
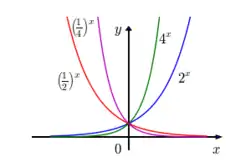

Exponenciální růst resp. exponenciální pokles je matematický model růstu resp. poklesu intenzity nějaké veličiny, který je vyjádřen pomocí exponenciální funkce času se základem vyšším resp. nižším než jedna. Označíme-li modelovanou veličinu v čase jako , pak pro platí rovnice:
- ,
kde je úroveň modelované veličiny v čase nula.
Pro a se dá odvodit, že modelovaná veličina se zdvojnásobí za dobu , tj. např. .
Pro a se dá odvodit, že modelovaná veličina klesne na polovinu za dobu , tj. např. .
Rychlost růstu resp. poklesu takto se chovající veličiny je úměrná její okamžité hodnotě; konkrétně platí diferenciální rovnice:
- .
Exponenciální růst se používá například na modelování prvotní fáze růstu populací bakterií v optimálním prostředí nebo jako základní model ekonomického růstu resp poklesu.
Literatura
- BARTSCH, Hans-Jochen. Matematické vzorce. 4. vyd. Praha: Academia, 1994. 832 s. ISBN 80-200-1448-9.