Kosinus

Kosinus je goniometrická funkce úhlu. Zapisuje se jako ${\displaystyle \cos \varphi }$, kde ${\displaystyle \varphi }$ je velikost úhlu. Pro ostré úhly je definována v pravoúhlém trojúhelníku jako poměr přilehlé odvěsny a přepony (nejdelší strany). Alternativně lze kosinus definovat jako posunutí sinu po ose ${\displaystyle x}$ vlevo o úhel ${\displaystyle {\frac {\pi }{2}}}$ , tj. ${\displaystyle \cos x=\sin({\frac {\pi }{2}}-x)}$. Definici lze konzistentně rozšířit jak na všechna reálná čísla, tak i do oboru komplexních čísel.

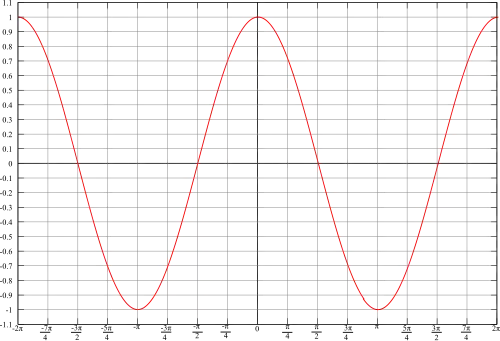
Funkce ${\displaystyle y=\cos x\,\!}$ má následující vlastnosti (kde ${\displaystyle k}$ je libovolné celé číslo):

• Definiční obor: ${\displaystyle \mathbb {R} }$ (reálná čísla)
• Obor hodnot: ${\displaystyle \langle -1;1\rangle }$
• Rostoucí: v každém intervalu ${\displaystyle \left(\pi +2k\pi ,2\pi +2k\pi \right)}$
• Klesající: v každém intervalu ${\displaystyle \left(2k\pi ,\pi +2k\pi \right)}$
• Maximum: +1 v bodech ${\displaystyle 2k\pi }$
• Minimum: −1 v bodech ${\displaystyle \pi +2k\pi }$
• Derivace: ${\displaystyle (\cos x)'=-\sin x\,\!}$
• Integrál: ${\displaystyle \int \cos x\,\mathrm {d} x=\sin x+c}$
• Taylorův polynom: ${\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}=\sum _{n=0}^{\infty }{\frac {(-x^{2})^{n}}{(2n)!}}}$
• Inverzní funkce (na intervalu ${\displaystyle \langle -1;1\rangle }$ a oborem hodnot ${\displaystyle \textstyle \left\langle 0,\pi \right\rangle }$: Arkus kosinus (arccos)
• Grafem funkce je kosinusoida.
• Kosinus dvojnásobného argumentu: ${\displaystyle \cos(2x)=\cos ^{2}x-\sin ^{2}x}$
• je:
  • sudá
  • omezená shora i zdola
  • periodická s periodou ${\displaystyle 2k\pi }$

Funkce kosinus je v komplexních číslech definována součtem řady

${\displaystyle \cos z=1-{\frac {z^{2}}{2!}}+{\frac {z^{4}}{4!}}-{\frac {z^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n}}{(2n)!}}}$

která konverguje na celé komplexní rovině. Pro každá dvě komplexní čísla z₁,z₂ platí:

${\displaystyle \cos z={\frac {e^{iz}+e^{-iz}}{2}},}$

${\displaystyle \cos \left(z_{1}+z_{2}\right)=\cos z_{1}\cos z_{2}-\sin z_{1}\sin z_{2},}$

${\displaystyle \cos iz=\cosh z,\,}$

Tyto vzorce plynou přímo z příslušných definičních mocninných řad daných funkcí. Kosinus je na celé komplexní rovině jednoznačná holomorfní funkce.

Kosinus se jednoduše definuje na jednotkové kružnici (kružnici se středem v počátku a s poloměrem 1): Je-li α úhel, který má počáteční rameno v kladné poloose x a je orientovaný od kladné poloosy x proti směru hodinových ručiček, je cos α roven x-ové souřadnici průsečíku této kružnice s koncovým ramenem úhlu α, jinak řečeno, rovná se (v absolutní hodnotě) délce úsečky z počátku k patě kolmice spuštěné z tohoto průsečíku na osu x. Délce této kolmice, přesněji (s ohledem na znaménko) y-ové souřadnici průsečíku jednotkové kružnice s koncovým ramenem úhlu α, je pak roven sin α.

Poloměr, kolmice a tato úsečka tvoří pravoúhlý trojúhelník, pro nějž platí Pythagorova věta, takže platí:

${\displaystyle (\sin \alpha )^{2}+(\cos \alpha )^{2}=1}$.

Na jednotkové kružnici je také vidět, že kosinus je v prvním a čtvrtém kvadrantu nezáporný (≥ 0), kdežto ve druhém a třetím nekladný (≤ 0). V prvním a druhém kvadrantu je klesající, ve třetím a čtvrtém rostoucí.

Orientovaný úhel lze rozšířit na všechna reálná čísla předpisem ${\displaystyle \alpha +k\cdot 2\pi }$ v úhlové míře resp. ${\displaystyle \alpha +k\cdot 360^{\circ }}$ v míře stupňové, kde ${\displaystyle k}$ je celé číslo. Kosinus lze tedy konzistentně definovat jako funkci na celé množině reálných čísel.

• Kosinová věta
• Sinus
• Trigonometrie
• Goniometrie
• Goniometrické funkce

• Obrázky, zvuky či videa k tématu kosinus na Wikimedia Commons
• Slovníkové heslo kosinus ve Wikislovníku