Brahmaguptův vzorec

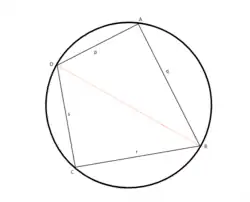
Brahmaguptův vzorec (podle indického matematika Brahmagupty) umožňuje vypočítat obsah S tětivového čtyřúhelníka, tedy takového, kterému může být opsána kružnice. Nechť ABCD je tětivový čtyřúhelník se stranami a, b, c a d, pak platí:

${\displaystyle S={\sqrt {(s-a)(s-b)(s-c)(s-d)}}}$,

kde s je polovina obvodu tohoto čtyřúhelníka:

${\displaystyle s={\frac {a+b+c+d}{2}}.}$

Brahmaguptův vzorec lze dokázat aplikací Heronova vzorce na dva trojúhelníky, na které lze čtyřúhelník rozdělit.

Pokud jedna ze stran má nulovou délku (např. 'd'), dostaneme Heronův vzorec pro obsah trojúhelníka:

${\displaystyle S={\sqrt {s(s-a)(s-b)(s-c)}}.}$

Z nerovnosti mezi aritmetickým a geometrickým průměrem plyne, že tětivový čtýřúhelník s daným obvodem má největší obsah, právě když má shodné strany, tj. je to čtverec.

Zobecněním Brahmaguptova vzorce na obecné rovinné čtyřúhelníky je Bretschneiderův vzorec:

${\displaystyle S={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\cos ^{2}\theta }},}$

kde ${\displaystyle \theta }$ je polovina součtu dvou protilehlých úhlů čtyřúhelníka.